 | 
|
Consequences Of Time Dependent Nuclear Decay Indices On Half Lives
| |
Theodore W. Rybka, Ph.D.
IMPACT
No. 106, April 1982
|  | 
I. Background And History
Early work in nuclear physics [1], [2], [3], [4] indicated that the nuclear decay parameter, l, was a constant. It was and still is generally believed that this decay rate is unaffected by changes in external parameters such as pressure, temperature, electromagnetic fields, and differing chemical environments. It is believed that radioactivity is a spontaneous, random event. The fundamental assumption made is that the decay of an atom is independent of the age of that atom.[5]
A brief look at a few nuclear physics texts [6], [7], [8] shows that at best the precision of nuclear decay parameters is known only to three significant figures and in some cases to four. Hence experimental data permits the possibility of a slight variation in the nuclear decay parameter. This variation could be as much as one part per thousand per year. Measurement of nuclear disintegration parameters has been done for about fifty years. To my knowledge no major research effort has been mounted to determine whether nuclear decay parameters vary at all with time. Once values of the decay index for a particular nuclide are obtained and a particular value is agreed upon, this value is generally accepted. Usually no further measurements are taken. The terminology is such that no change with time is expected. Note the quantity,l, is called the nuclear decay constant. Hence it is easy to see why a slight change in decay rate, if it exists, could have been overlooked during the past fifty years. 
II. The Case For Changing Nuclear Decay Parameter
A. External parameters. External parameters can effect slight changes in the nuclear decay rate.[9] DeYoung [10] has listed variations of up to 5%. B. Dudley's hypothesis. [11] Dudley rejects the idea that radioactive decay is completely spontaneous and instead hypothesizes that neutrinos from the neutrino sea, which has been suggested by others, trigger radioactive decay. C. Radiohalos. Radiohalos are minute concentric rings of discoloration in minerals such as mica formed by alpha ray bombardment from radioactive inclusions. Radiohalos give evidence that decay rates vary with time.[12], [13] Some researchers believe otherwise. D. The speed of light may have been faster in the past. Morton has proposed that the permittivity of free space has changed. [14] It then follows that the speed of light has changed. Furthermore, in the case of beta emission, Morton derives a relation between the nuclear decay parameter and the permittivity. If the permittivity has changed, it follows that the nuclear decay parameter has changed. Some investigators claim that there appears to be experimental evidence that the speed of light decreased in the past although the speed of light is constant at the present time. If this is true they argue in the following manner. The energy of emitted particles from the nucleus is related to the velocity of light through the relativistic expression for kinetic energy and the half life of a radioactive atom is related to the energy of the ejected particle by means of the empirical relation called the Geiger-Nuttal law. Through these relations we can deduce that if the speed of light is slowing down, then the radioactive decay rate is also slowing down. E. Observed values of half lives. There is a very wide dynamic range of half lives. The longest are about 109 (one billion) years. Some examples are the half life of U235 which is 0.7 x 109 years, the half life of U238 which is 4.5 x 109 years and the half life of Th232 which is 14.9 x 109 years. At the other extreme examples of radioisotopes with very short half lives are Po211 which has a half life of 1.64 x 10-4 seconds and At2l6 which has a half life of 3 x 10-4 seconds. The radioisotope carbon 14 which is used in radiometric dating has a half life which is not that precisely known. Values ranging from 5570 to 5730 years have appeared in the literature, with the larger values being the more recent ones. Note that the neutron in the environment of the nucleus is a stable particle, but as a free particle the neutron has a half life of eight minutes. Thus the environment of the nucleus is extremely important. Examination of the published half lives of long-lived radioisotopes indicates a precision of about one part per thousand. Two cases where it appears that the half life is increasing with time are as follows. Glasstone[15] (1950) has the half life for Protactinium 231 as 3.2 x 104 years while Kaplan [16] (1962) has the half life as 3.43 x 104 years. For the half life of Radium 223, Glasstone has 11.2 days while Kaplan has 11.68 days. 
III. Theory
Consider the following three cases: (1) the disintegration index l , is constant; (2) the disintegration index, l , varies linearly with time; and (3) the disintegration index, l , varies exponentially with time. Each case will result in a corresponding mathematical expression which can be solved for the number of radioactive atoms present at a particular time. From these solutions, expressions can be derived for the half life, t1/2. The mathematical expressions for the previously mentioned quantities are developed in the Appendix. The constant part of the nuclear decay parameter is a . Calling this the nuclear "decay constant" the figure is a plot of the half life versus the "decay constant." The half life of a radionuclide is determined by the time t it takes for the parent material to be reduced to one half of its original value. Once the half life is found, users of the radiometric dating technique, take the expression for half life deduced by going forward in time and apply it to events which are reached by going backward in time. One ought to determine the half life by finding the time required to double the parent material if one goes backward in time. It is true, of course, that for a constant disintegration index, the half life computed by both methods is identical. However, for a variable disintegration index, the two expressions are significantly different. 
IV. Analysis
Plots of equations 3, 8, and 9 of the Appendix are shown of t1/2 versus a in the figure. The important radionuclides in radiometric dating are U238, K40, Ru87, and C14. They are said to have half lives of 4.5 billion years, 1.2 billion years, 50 billion years, and 5.73 thousand years respectively. The figure indicates the values for the half lives for these radionuclides for linear and exponential variation. The plot shows that for extremely low values of a in the exponential case, the half life is reduced orders of magnitude. For an exponential variation U238 does not have a half life of 4.5 billion years but only around 10,000 years. For large values of a , the half life of the exponential variation is the same as for the constant case. Note that b = .001 was used. For smaller values of b , the values of t1/2 are the same for even smaller values of a but when a is small enough, the t1/2 value for the exponential variation deviates from the straight line plot and becomes significantly smaller. 
V. Conclusion
If a small amount of exponential variation occurs in the nuclear decay index, then the half lives of the radiometric nuclides are drastically reduced-orders of magnitude. In the case of U238 the half life is reduced by a factor of 10 5. Hence the whole area of radiometric dating ought to be rethought. The reason that there is such a great change in half life due to a minuscule change in decay index is due to the extrapolation technique of radiometric dating. When one uses the radiometric dating technique, one extrapolates from a time base of days at most to billions of years. The extrapolation factor in time is approximately 1011. Any competent experimentalist knows that extrapolation by such a large factor is very poor technique. Hence one should expect the radiometric dating technique to run into formidable problems. There appears to be a difficulty in this approach when one considers carbon 14. For the linear case the calculated half life is approximately one half of the currently accepted half life and in the exponential case it is approximately one third. The carbon 14 method generally agrees quite well with historical dates. Perhaps the assumed time dependence should be reduced more—say by a factor of 10. Then the calculated carbon 14 half life for the exponential case is only 1.4 times less than the currently accepted value. The literature should be thoroughly researched for published values of nuclear decay parameters to determine whether any long-term variation with time exists. In addition, recent measurements of half lives should be made and then compared to measurements taken much earlier in time.

| References
1. Kaplan, I., Nuclear Physics, Addison-Wesley, 1962, p. 231. Return to Text
2. Richtmyer, F.K., E.H. Kennard, and J.N. Cooper, Introduction To Modern Physics, 6th ed., McGraw-Hill, 1969, p. 215. Return to Text
3. Halliday, D., lntroductory Nuclear Physics, 2nd ed., John Wiley & Sons, 1955, p. 66. Return to Text
4. Evans, R.D., The Atomic Nucleus, McGraw-Hill, 1955, p. 470. Return to Text
5. Ibid., p. 471. Return to Text
6. Kaplan, pp. 248-250. Return to Text
7. Richtmyer, et al., p. 219. Return to Text
8. Halliday, p. 64. Return to Text
9. Anderson, J.L., and G.W. Spangler, "Radiometric Dating: Is the 'Decay Constant' Constant?", Pensee, V. 4, No. 4, Fall 1974, p. 31. Return to Text
10. DeYoung, D.B., "The Precision of Nuclear Decay Rates," Creation Research Society Quarterly, V. 13, June 1976, p. 38. Return to Text
11. Slusher, Harold S., Critique of Radiometric Dating, ICR Technical Monograph No. 2, 2nd ed., 1981, p. 20. Return to Text
12. Ibid., pp. 25-26. Return to Text
13. Gentry, R.V., "On the lnvariance of the Decay Constant Over Geologic Time," Creation Research Society Quarterly, V. 5, No. 2, 1968, p. 83. Return to Text
14. Morton, G.R., "Electromagnetics and the Appearance of Age, "Creation Research Society Quarterly, March 1982. Return to Text
15. Glasstone, S., "The Sourcebook on Atomic Energy, " Van Nostrand, 1950, pp. 125-128. Return to Text
16. Kaplan, p. 249. Return to Text
 | Appendix
A. For a constant disintegration index. Radioactive nuclei are said to obey the following differential equation,
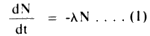
where l, the disintegration index is a constant and 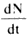 is the rate at which nuclei are disintegrating to form a new type of nucleus. is the rate at which nuclei are disintegrating to form a new type of nucleus.
Solving the differential equation gives,
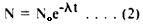
where N0 is the intial number of parent nuclei and N is the number of parent nuclei at any time t. The half life, t1/2 is given by,
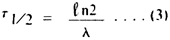
B. For a linear variation of disintegration index. For a linear variation the form for l becomes 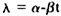
where a and b are constants. Then the decay rate becomes,
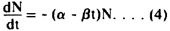
Note that the decay rate decreases with time. The solution of this differential equation is,
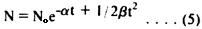
C. For an expontential variation of the disintergration index. For an expontential variation the form for l becomes 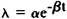
where a and b are constants. Then the decay rate becomes,
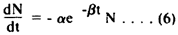
Note that the decay rate decreases with time. The solution of this differential equation is,
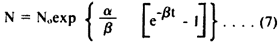
D. Half life determination.
1. For linear variation case. When N0=2N, t = -t1/2 Set these relations into equation (5). Obtain,
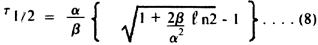
2. For expontential variation case. Set N=2N0 and t = -t1/2 into equation (7). Obtain,
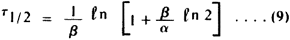

|
"Vital Articles on Science/Creation"
April 1982
Copyright © 1982 All Rights Reserved |
 |

